振动筛的结构、特点和力学模型
作者:宏源科技 日期:2014-04-17
为了便于分析、研究,有必要对新旧两种类型的振动筛从结构上和力学模型上进行分析对比。
1. 1 传统的振动筛的结构、特点和力学模型
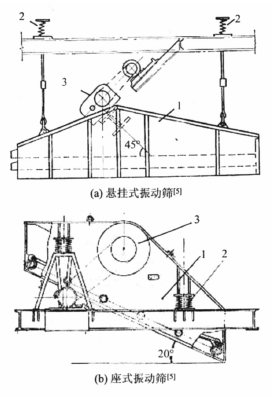
目前,广泛使用的振动筛的结构如图1 所示[8]。
图1( a) 为挂式振动筛,图1( b) 为座式振动筛。 筛箱与水平面的倾角为15° - 20°,上面固定有筛网和激振器,筛面可以是单层或多层。筛箱通过弹簧 悬挂或安装在机架上。电机通过皮带传动,带动固定于筛箱上的激振器,从而使筛箱产生振动而工作。
上述两种结构振动筛的力学模型简化成以下两 种形式[8],见图2。
本文基于机械本质安全的角度考虑,研究提出 新型振动筛的结构形式如图3 所示。新旧两种筛的 区别,可通过比较图1、图3 两种振动筛的结构或图 2 和图4 的力学模型图可知,传统结构振动筛图1 的激振器是安装在筛箱上的,而作者提出的新型振 动筛图3 的激振器和筛箱是分离的,他们之间通过 弹簧联接,使其转变为双自由度振动筛,其他不变。
为了便于研究和利用数学工具进行分析计算, 可以把新型振动筛的力学模型抽象简化为如图4 所 示的二自由度受迫振动系统。图4 中,( a) 为吊式 筛力学模型,( b) 为座式筛力学模型。
图4 中,设m1—筛箱参振质量( 包括物料的粘 着质量) ; m2—激振器( 及其机架) 参振质量; k1—激 振器与筛箱的联接弹簧的弹簧刚度; k2—机架与激 振器之间的联接弹簧的弹簧刚度; c1—激振器与筛 箱的联接弹簧的线性阴尼系数; c2—机架与激振器之间的联接弹簧线性阴尼系数; ωm1—由m1 和k1 构 成的系统的固有频率; ωm2—由m2 和k2 构成的系统 的固有频率; 则有: ωm1 = k1 槡m1 k1 = ωm1 × m1 ( 1) ωm2 = k2 槡m2 k2 = ω2 m2 × m2 ( 2) 从图4 中可见,双自由度振动筛的力学模型为 二自由度系统的受迫振动。
1. 1 传统的振动筛的结构、特点和力学模型
目前,广泛使用的振动筛的结构如图1 所示[8]。
图1( a) 为挂式振动筛,图1( b) 为座式振动筛。 筛箱与水平面的倾角为15° - 20°,上面固定有筛网和激振器,筛面可以是单层或多层。筛箱通过弹簧 悬挂或安装在机架上。电机通过皮带传动,带动固定于筛箱上的激振器,从而使筛箱产生振动而工作。
上述两种结构振动筛的力学模型简化成以下两 种形式[8],见图2。

1 - 筛箱; 2 - 弹簧2; 3 - 激振器架; 4 - 激振器; 5 - 弹簧
图3 双自由度振动筛结构图
1. 2 新型振动筛的结构、特点和力学模型本文基于机械本质安全的角度考虑,研究提出 新型振动筛的结构形式如图3 所示。新旧两种筛的 区别,可通过比较图1、图3 两种振动筛的结构或图 2 和图4 的力学模型图可知,传统结构振动筛图1 的激振器是安装在筛箱上的,而作者提出的新型振 动筛图3 的激振器和筛箱是分离的,他们之间通过 弹簧联接,使其转变为双自由度振动筛,其他不变。
为了便于研究和利用数学工具进行分析计算, 可以把新型振动筛的力学模型抽象简化为如图4 所 示的二自由度受迫振动系统。图4 中,( a) 为吊式 筛力学模型,( b) 为座式筛力学模型。
图4 中,设m1—筛箱参振质量( 包括物料的粘 着质量) ; m2—激振器( 及其机架) 参振质量; k1—激 振器与筛箱的联接弹簧的弹簧刚度; k2—机架与激 振器之间的联接弹簧的弹簧刚度; c1—激振器与筛 箱的联接弹簧的线性阴尼系数; c2—机架与激振器之间的联接弹簧线性阴尼系数; ωm1—由m1 和k1 构 成的系统的固有频率; ωm2—由m2 和k2 构成的系统 的固有频率; 则有: ωm1 = k1 槡m1 k1 = ωm1 × m1 ( 1) ωm2 = k2 槡m2 k2 = ω2 m2 × m2 ( 2) 从图4 中可见,双自由度振动筛的力学模型为 二自由度系统的受迫振动。
本文关键词:







