大型振动筛分机有限元计算精度与稳定性分析
作者:宏源科技 日期:2014-01-10
对大型复杂结构的动态特性分析,力学模型的建立是十分重要的。简化力学模 型时要考虑筛体实际结构和受力方式,使该力学模型能很好地反应结构的真实情 况。由于振动筛结构比较复杂,可以先在 Pro/E 中建立实体模型,再转到有限元分 析软件 ANSYS 中进行计算分析。由于两者之间接口的局限性,为避免实体数据信 息丢失,保证模型的准确性,最终确定为直接在 ANSYS 中建模并分析。
建立几何模型时,为了保持计算精度,并控制计算规模,需要对振动筛分机的结构 作适当的简化和变换处理。
有限元分析的目的是利用分析结果验证、修改并优化设计方案,所以保证精度与计算稳定性是建模首要考虑的问题。有限元分析是一个复杂的计算过程,计算结果精度与很多因素有关,因而对结果精度做出定量估计非常困难。通过误差分析,找出有限元分析过程中产生误差的原因,然后定性的提出提高结果精度的方法,使计算结果稳定可靠。
从有限元分析的整个过程来看,计算结果的误差主要来自两个方面:模型误差和计算误差。计算误差是利用计算机对模型进行数值计算时所产生的误差,误差的性质是舍入误差和截断误差,在此不作考虑,主要对模型误差进行分析。模型误差是指将实际问题抽象为适合计算机求解的有限元模型时所产生的误差,即有限元模型和实际问题之间的差异。产生这类误差的原因主要有以下三种。
(1)离散误差
有限元法是将一个连续的弹性体离散为由有限个单元组成的组合体,并在单元 内用一假设的插值函数逼近真实函数。这样插值函数与真实函数之间存在一定的差 异,即离散误差,其量级可以用式(5-51)来估计。 1 ( ) p m E O h + − = (5-51) 式中,h为单元特征长度尺寸; p 为单元多项式的最高阶次;m 为函数在泛函中的 最高阶倒数。从式(5-51)可知,离散误差的大小与单元尺寸和插值多项式的阶次有关。单元尺寸减小,插值函数的阶次增高,都将使误差减小,即,使有限元解收敛于精确解。因此式(5-51)也对有限元解的收敛速度做出了量级估计。
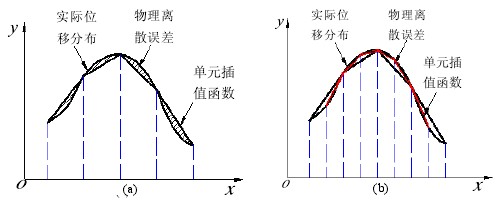
例如,对于三节点三角形位移单元,差值函数是线性函数,即 p = 1。由于在能 量泛函中只有位移函数本身,没有位移导数,即 m = 0,所以位移误差是 2 O ( h ),收 敛的速度也是 2 O ( h )。若用六节点三角形单元,差值函数是二次函数,则误差和收 敛速度的量级变为 3 O ( h )。因此,如果所有单元的尺寸都减半,则三节点单元的误 差级数为1 4,而六节点单元的误差级数为1 8。后者的收敛速度比前者要快一倍。 图 5-1 描述了单元尺寸和插值函数阶次对于离散误差的影响,(b)与(a)相比,说 明离散时所选取的单元尺寸减半或提高阶次,则误差精度将会减小,同时由式(5-51) 可知其收敛的速度增加。
进行有限元分析时,在分析结构与其它结构或外部环境的相互作用时,通过在模型上设置已知的边界条件来表示。将结构实际工况量化为模型边界条件时,两者之间可能存在一定的差异,即为边界条件误差。边界条件误差来自两个方面。第一是对实际工况进行定量表示时产生的,属于测量误差,有较大的偶然性。只有较准确地掌握实际受力大小、位移状态和温度分布才能减小这类误差。
第二类边界条件误差来自载荷的移置,这是有限元法离散所引起的。由于在有限元计算过程中,设置在模型上的所有非节点集中载荷、分布的棱边载荷、表面载荷以及体积力等都需要移置为等效的节点载荷,这与结构的实际载荷情况并不一致,因而也会带来一定的误差。根据圣维南原理,载荷移置仅对载荷附近的局部特性有影响,而对整个结构的力学性能影响不大。当需要考察结构在载荷附近的局部特性时,可以通过加密网格的方法来减小载荷移置的影响。
(3)单元形状误差
单元的网格形状对计算结果的误差大小有影响。如三节点三角形内部应力的误差可以用式(5-52)来估计: 2 E ≤ 4 M h / sinθ(5-52) 式中, 2 M 为真实位移场函数的二阶导数在单元上的最大模; h 为三角形的最大边 长;θ 为三角形的最大内角。
可以看出,当单元的三角形网格很“钝”时,最大内角θ 接近180o,sinθ 近似 为零。出现这种情况时,即使单元分得很小,应力误差仍可能非常大,所以在分网 时要尽量避免出现这类不规则的形状。单元形状对误差的影响一般限于单元内部或 相邻单元,因此当整个模型中存在少数形状较差的单元时,对整个模型的变形不会 影响太大,但对局部应力的影响较大,因此在应力集中时尽量划分比较规则的网格。
建立几何模型时,为了保持计算精度,并控制计算规模,需要对振动筛分机的结构 作适当的简化和变换处理。
有限元分析的目的是利用分析结果验证、修改并优化设计方案,所以保证精度与计算稳定性是建模首要考虑的问题。有限元分析是一个复杂的计算过程,计算结果精度与很多因素有关,因而对结果精度做出定量估计非常困难。通过误差分析,找出有限元分析过程中产生误差的原因,然后定性的提出提高结果精度的方法,使计算结果稳定可靠。
从有限元分析的整个过程来看,计算结果的误差主要来自两个方面:模型误差和计算误差。计算误差是利用计算机对模型进行数值计算时所产生的误差,误差的性质是舍入误差和截断误差,在此不作考虑,主要对模型误差进行分析。模型误差是指将实际问题抽象为适合计算机求解的有限元模型时所产生的误差,即有限元模型和实际问题之间的差异。产生这类误差的原因主要有以下三种。
(1)离散误差
有限元法是将一个连续的弹性体离散为由有限个单元组成的组合体,并在单元 内用一假设的插值函数逼近真实函数。这样插值函数与真实函数之间存在一定的差 异,即离散误差,其量级可以用式(5-51)来估计。 1 ( ) p m E O h + − = (5-51) 式中,h为单元特征长度尺寸; p 为单元多项式的最高阶次;m 为函数在泛函中的 最高阶倒数。从式(5-51)可知,离散误差的大小与单元尺寸和插值多项式的阶次有关。单元尺寸减小,插值函数的阶次增高,都将使误差减小,即,使有限元解收敛于精确解。因此式(5-51)也对有限元解的收敛速度做出了量级估计。
例如,对于三节点三角形位移单元,差值函数是线性函数,即 p = 1。由于在能 量泛函中只有位移函数本身,没有位移导数,即 m = 0,所以位移误差是 2 O ( h ),收 敛的速度也是 2 O ( h )。若用六节点三角形单元,差值函数是二次函数,则误差和收 敛速度的量级变为 3 O ( h )。因此,如果所有单元的尺寸都减半,则三节点单元的误 差级数为1 4,而六节点单元的误差级数为1 8。后者的收敛速度比前者要快一倍。 图 5-1 描述了单元尺寸和插值函数阶次对于离散误差的影响,(b)与(a)相比,说 明离散时所选取的单元尺寸减半或提高阶次,则误差精度将会减小,同时由式(5-51) 可知其收敛的速度增加。

图 5-1 离散误差的几何描述
(2)边界条件误差进行有限元分析时,在分析结构与其它结构或外部环境的相互作用时,通过在模型上设置已知的边界条件来表示。将结构实际工况量化为模型边界条件时,两者之间可能存在一定的差异,即为边界条件误差。边界条件误差来自两个方面。第一是对实际工况进行定量表示时产生的,属于测量误差,有较大的偶然性。只有较准确地掌握实际受力大小、位移状态和温度分布才能减小这类误差。
第二类边界条件误差来自载荷的移置,这是有限元法离散所引起的。由于在有限元计算过程中,设置在模型上的所有非节点集中载荷、分布的棱边载荷、表面载荷以及体积力等都需要移置为等效的节点载荷,这与结构的实际载荷情况并不一致,因而也会带来一定的误差。根据圣维南原理,载荷移置仅对载荷附近的局部特性有影响,而对整个结构的力学性能影响不大。当需要考察结构在载荷附近的局部特性时,可以通过加密网格的方法来减小载荷移置的影响。
(3)单元形状误差
单元的网格形状对计算结果的误差大小有影响。如三节点三角形内部应力的误差可以用式(5-52)来估计: 2 E ≤ 4 M h / sinθ(5-52) 式中, 2 M 为真实位移场函数的二阶导数在单元上的最大模; h 为三角形的最大边 长;θ 为三角形的最大内角。
可以看出,当单元的三角形网格很“钝”时,最大内角θ 接近180o,sinθ 近似 为零。出现这种情况时,即使单元分得很小,应力误差仍可能非常大,所以在分网 时要尽量避免出现这类不规则的形状。单元形状对误差的影响一般限于单元内部或 相邻单元,因此当整个模型中存在少数形状较差的单元时,对整个模型的变形不会 影响太大,但对局部应力的影响较大,因此在应力集中时尽量划分比较规则的网格。
本文关键词:










